Instrumental Variables
In this third post, I want to go into the details of a method mentioned in my previous post about Structural Causal Modeling called Instrumental Variables (IV). IVs have traditionally been used to estimate structural econometric models, but during the last decade, advocates have encouraged the broader use of IVs within social sciences (Bollen, 2012; Sovey & Green, 2011). One of its interesting characteristics is that IVs allow researchers to estimate causal relationships when randomized experiments are not feasible, so we need to use observational data.
Instrument
We can observe the setup of an IV \( (I) \) in Figure 1. As researchers, let’s say that we are interested in calculating the causal effect of \( X \) on \( Y \) \( (X \rightarrow Y) \). From our understanding of causal models, to know the correct causal effect of \( X \rightarrow Y \), we need to control for the confounders (in this case represented by the set of variables \( U \)) because if we don’t, there will be confounder bias in our estimation. But what can we do if the set of variables \( U \) is unobserved? Well, IVs allow us to estimate the causal effect of \( X \) on \( Y \) without measuring the set of confounders \( U \) as long as we can define the instrument variable \( I \). The variable \( I \) is an instrument if:
- \( I \) defines a causal relationship with \( X \).
- \( I \) affects to the outcome variable \( Y \) only through its effect on \( X \) (exclusion restriction).
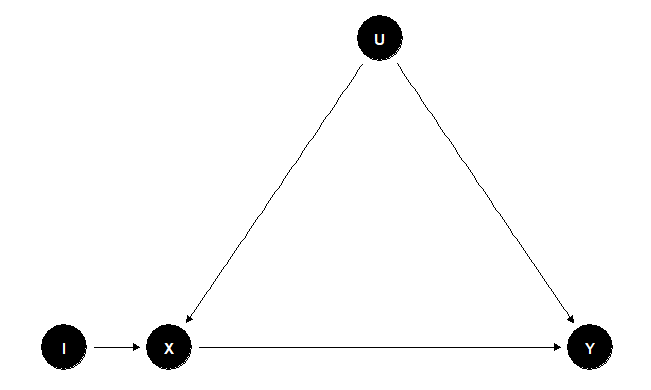
Figure 1
To illustrate a practical example of using IVs, let’s look at the work done by Coviello et al. (2014). In this paper, the authors studied the process of emotional contagion in a massive social network site; they wanted to know if the online emotional expression of users on Facebook affects the emotions their friends share on the same platform. To simplify the example with a particular case and following the setup of Figure 1, the variable \( X \) is defined as the average emotional expression of Yvonne’s friends’ status on Facebook, and variable \( Y \) is the emotional expression of Yvonne. Both \( X \) and \( Y \) are measured in the same period. For the instrument \( I \), a variable is needed that (1) defines a causal relationship with the emotional expression of Yvonne’s friends and (2) follows the exclusion restriction (affects Yvonne’s emotional expression through the emotions of her friends). The researchers picked rainfall as instrument \( I \); their justification was that if there is a relationship between rainfall and emotion expression, it must be \( rainfall \rightarrow emotion \) because emotions can’t affect rainfall; this rationale complies with (1). For the exclusion restriction (2), they computed the model when there was no rainfall in Yvonne’s city, so the instrument had no relationship with her emotional expression. The final general result showed that rainfall directly influences the emotional content status messages of users on Facebook, and it also affects the status messages of friends in cities that are not experiencing rainfall.
Analysis
The analysis of causal effects using IVs uses the additive properties of SEM to calculate the causal effect when we can define an instrument.
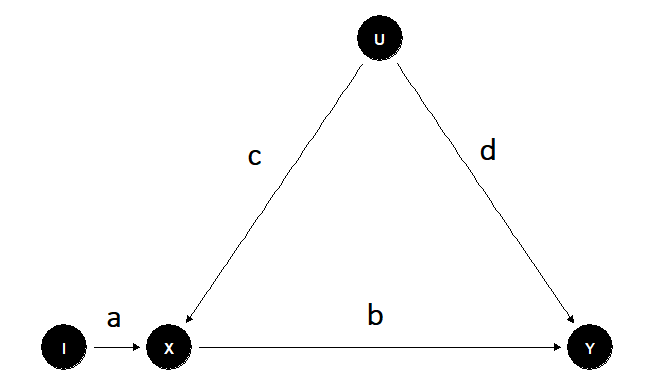
Figure 2
We already know that Figure 2 represents a setup for IVs. Here, we are interested in the causal effect of \( X \) on \( Y \). The variable \( I \) is a well-defined instrument, the set \( U \) represents the group of unobserved confounding variables, and a, b, c, and d the causal effects of the DAG assuming linear equations (if you need to refresh concepts like confounders or DAG take a look at my previous post).
Because \( I \) and \( X \) are unconfouded the causal effect of \( I \) on \( X \) can be estimated from the regression
\[ X = a I + error_1 \tag{1} \]
Likewise, the variables \( I \) and \( Y \) are unconfounded because the path \( I \rightarrow X \leftarrow U \rightarrow Y \) is blocked in the collider \( X \). So the estimate of the regression of \( I \) on \( Y \) will be equal to the direct effect on the path \( I \rightarrow X \rightarrow Y \), which is the product of the path coefficients \( ab \).
Since we estimated the values \( a \) and \( ab \). The causal effect \( b \) from \( X \) to \( Y \) can be obtained by dividing the previous estimations \( b=ab/a \) (Pearl & Mackenzie, 2018)
Limitations
Even though using IV might seem a good approach to fixing problems as confounding issues, the truth is that instruments can be very difficult to find. Researchers cannot use the actual data to find IVs; the knowledge about theory and the model derived from it is key to defining a valid IV for the problem under investigation. A well-defined IV should not be affected by other variables in the model; this can’t be proved, so it is based on the knowledge of the system studied. The correlation between the IV and \( X \) must be significant because weak correlations can lead to misleading parameter estimates and standard errors.
An Instrumental Variable Example
I present an example of Instrumental Variables with simulated data to show how to implement the previous analysis. The process has the following steps:
- Plot the IV model.
- Data simulation of the DAG defined.
- Check correlation between instrument \( I \) and variable \( X \).
- Estimate the causal effect of the IV model.
- Show the estimation mistakes if we don’t use IV for this example.
Step 1
First we load the packages needed to create the example and plot theDAG.
#We load the package dagitty to create the IV modellibrary(dagitty)#Definition of the DAGg <- dagitty("dag { X [pos="0,0"] I [pos="-1,0"] Y [pos="4,0"] U [pos="2,2"] W [pos="2,-2"] I -> X -> Y U -> X U -> Y W -> X W -> Y}")#We load the package ggdag to plot the DAGlibrary(ggdag)#Plot the DAGggdag(g) + theme_dag_blank()Step 2
Based on the model previously defined we simulate the theoretical data.In this case we interested in the causal effect of X on Y, the variableI is the instrument, and variables U and W are unobserved confounders.
#We load the package lavaan to simulate the data library(lavaan)#Simulated model (effects of exogenous variables are set to be non-zero)lavaan_model <- "X ~ .5*I + .4*U + .4*W Y ~ .7*X + .1*U + .4*W"#Data consistent with the simulated model with 1000 observationsset.seed(1234)g_tbl <- simulateData(lavaan_model, sample.nobs=1000)#Show the first rows of simulated datahead(g_tbl)## X Y I U W## 1 -1.4189076 -1.9098602 0.23531557 0.9724314 -1.32087141## 2 -0.2432510 0.8651646 -0.01304215 0.1341461 0.09257077## 3 1.5269161 1.2851663 1.40818583 0.8286825 -0.59320416## 4 -2.0031355 -2.8247830 -1.68911977 -2.8507097 -1.66129610## 5 0.4566986 1.2465048 -1.68652731 0.8188786 -0.57662826## 6 1.6487979 -0.1609893 0.75620545 1.4406250 -1.04088989Step 3
In order to check if the simulation created a good instrument I measurethe correlation between I and X.
#Correlation checkcor.test(g_tbl$I,g_tbl$X)## ## Pearson"s product-moment correlation## ## data: g_tbl$I and g_tbl$X## t = 13.199, df = 998, p-value < 2.2e-16## alternative hypothesis: true correlation is not equal to 0## 95 percent confidence interval:## 0.3314420 0.4370615## sample estimates:## cor ## 0.3855139Step 4
Now we estimate the causal effect using instrumental variables via twodifferent methods available in R. First, we used the two stage leastsquares method step by step. Second, we used the package ivpack specificfor IVs.
#Two stageleast squares#First step by step#Stage 1: Regress X on Is1 <- lm(X ~ I, data = g_tbl)#Get predicted value of X given Ipredx <- predict(s1, type="response")#Stage 2: Regress Y on predicted values of Xs2 <- lm(g_tbl$Y ~ predx)#Summary the resultssummary(s2)## ## Call:## lm(formula = g_tbl$Y ~ predx)## ## Residuals:## Min 1Q Median 3Q Max ## -5.1899 -0.9990 0.0060 0.9992 4.7011 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.008825 0.046668 0.189 0.85 ## predx 0.699069 0.099702 7.012 4.34e-12 ***## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## Residual standard error: 1.467 on 998 degrees of freedom## Multiple R-squared: 0.04695, Adjusted R-squared: 0.04599 ## F-statistic: 49.16 on 1 and 998 DF, p-value: 4.337e-12The result shows that the estimated causal effect is approx 0.7 which isthe value we simulate so the use of Iv in this case allow us to computea causal effect pretty close to the real one simulated but withoutconsidering the unobserved confounders. Let’s see what are the resultsusing the package ivpack
#Two least squares using ivpack#We load the package ivpack library(ivpack)#we compute the causal IV model specifying the regression and the instrumentivmodel <- ivreg(Y ~ X, ~ I, data=g_tbl) #summary results showing standard errorsrobust.se(ivmodel)## [1] "Robust Standard Errors"## ## t test of coefficients:## ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.0088247 0.0344555 0.2561 0.7979 ## X 0.6990690 0.0714531 9.7836 <2e-16 ***## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1From this result we obtained the same value for the causal effect of Xon Y from the previous calculation but the package ivpack also give usthe standard errors.
Step 5
To show the mistakes we can made in the case of not defining aninstrument. We calculate the effect of X on Y directly and the effect ofX on Y when we can measure U and W
#Effect of X on Y with without instrument Isummary(lm(Y ~ X, data = g_tbl))## ## Call:## lm(formula = Y ~ X, data = g_tbl)## ## Residuals:## Min 1Q Median 3Q Max ## -3.5005 -0.7308 -0.0406 0.7581 3.0766 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.01850 0.03345 0.553 0.58 ## X 0.88400 0.02770 31.917 <2e-16 ***## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## Residual standard error: 1.057 on 998 degrees of freedom## Multiple R-squared: 0.5051, Adjusted R-squared: 0.5046 ## F-statistic: 1019 on 1 and 998 DF, p-value: < 2.2e-16We can see that the estimate of the causal effect of X on Y is wrong inthis case because 0.88 is far from the simulated 0.7
#Effect of X on Y in case we can measure U and Wsummary(lm(Y ~ X + U + W, data = g_tbl))## ## Call:## lm(formula = Y ~ X + U + W, data = g_tbl)## ## Residuals:## Min 1Q Median 3Q Max ## -3.0141 -0.6737 0.0037 0.6703 3.3444 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.01011 0.03122 0.324 0.746134 ## X 0.73480 0.02906 25.283 < 2e-16 ***## U 0.11501 0.03281 3.505 0.000476 ***## W 0.40206 0.03337 12.047 < 2e-16 ***## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## Residual standard error: 0.9858 on 996 degrees of freedom## Multiple R-squared: 0.5702, Adjusted R-squared: 0.5689 ## F-statistic: 440.5 on 3 and 996 DF, p-value: < 2.2e-16Results
In this example we shown that when we define an instrumental variable itis possible to obtain a good estimate of the causal effect under studyeven if we can’t measure confounded variables.
References
Bollen, K. A. (2012). Instrumental Variables in Sociology and the Social Sciences. Annual Review of Sociology, 38(1), 37–72. https://doi.org/10.1146/annurev-soc-081309-150141
Coviello, L., Sohn, Y., Kramer, A. D., Marlow, C., Franceschetti, M., Christakis, N. A., & Fowler, J. H. (2014). Detecting emotional contagion in massive social networks. PloS One, 9(3), e90315. https://doi.org/10.1371/journal.pone.0090315
Pearl, J., & Mackenzie, D. (2018). The Book of Why: The New Science of Cause and Effect. Basic Books.
Sovey, A. J., & Green, D. P. (2011). Instrumental Variables Estimation in Political Science: A Readers’ Guide. American Journal of Political Science, 55(1), 188–200. https://doi.org/10.1111/j.1540-5907.2010.00477.x
