Structural Causal Modeling

In this second post, I want to describe a method developed by Judea Pearl called Structural Causal Modeling (SCM). Based on his previous work on Bayesian Networks and machine learning, since the 1980s, Professor Pearl developed the SCM framework using elements of graph theory to elaborate causal models. Moreover, this method integrates the Potential Outcome Model (POM) and Structural Equation Modeling (SEM) into a single framework.

SCM was developed using graph theory; thus, its visual representation is a graph where causal hypotheses are presented as directed arrows between observed or latent variables. Because the possibilities are exponentially unwieldy when we elaborate on directed graphs, this method has to deal with different structures of intermediate variables. The role of mediators, confounders, and colliders on causal paths must be treated carefully because they might affect or even eliminate the causal effect under analysis. Finally, it is important that SCM requires researchers to elaborate their models based on theoretical grounds; each directed link that establishes a causal relationship between variables must be justified under logical assumptions.

Directed Acyclic Graphs

Before I move forward with the explanation of SCM, I would like to take a quick look at the concept of directed acyclic graphs (DAG). In DGAs, the variables are referred to as nodes or vertices. These variables are connected by edges or links that establish dependencies between them. We say that a pair of nodes is related (adjacent) if a link connects them. The direction of the link represented by an arrow (\( \longrightarrow \)) determines what node is the cause and what is the effect; the direct causes of a variable are called parents, while all variables caused by another one are its children. The absence of an arrow between a pair of variables reflects the hypothesis that no causal effect exists between them. DAGs do not have paths that start and end in the same node (cycles). In Figure 1, you can see an example of a DAG.

Tred-G

Figure 1

SCM

The Structural Causal Model developed by Pearl combines elements of structural equation models, the potential outcome framework, and graphical models developed for probabilistic reasoning (Bayesian networks) and causal analysis (Pearl, 2009). The framework addresses fundamental challenges in causal inference due to the following list of features (Kline, 2015):

      1. Causal hypotheses are represented both graphically and in expressions that are a mathematical language subject to theorems, lemmas, and proofs.
      2. The SCM provides a precise language for communicating the assumptions behind causal questions to be answered.
      3. The SCM explicitly distinguishes between questions that can be empirically tested versus those that are unanswerable, given the model. It also provides ways to determine what new measurements would be needed to address an “unanswerable” question.
      4. Finally, the SCM subsumes other useful theories or methods for causal inference, including the potential outcomes model and SEM.

    As SCM represents a causal network graph, there are three basic building blocks that characterize all possible patterns of arrows in the network:

    In Figure 5, we can see that the instrument \( I \) allows us to obtain the effect of \( I \) in \( X \) directly; then, we also can compute the effect of \( I \) on \( Y \) through \( X \) because the path \( I \rightarrow X \leftarrow U \rightarrow Y \) is blocked by the collider \( X \). With these results, it should be possible to “factor” the effect of \( X \) on \( Y \)

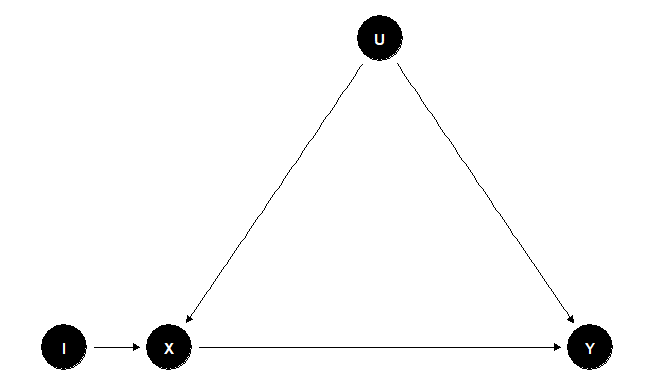
    Figure 5

    Limitations

    The main assumption of an SCM is that models must be created based on theoretical grounds. By combining models, structural equations, and observational data, researchers should be able to draw causal conclusions as long as they defend the logic of their assumptions. However, causal claims seem to be avoided by researchers since structural equations in SEM became an issue of the model adjustment than the theoretical implications behind it. Data can give researchers estimates but it cannot tell the reason why for those measures.

    A Back-door Example

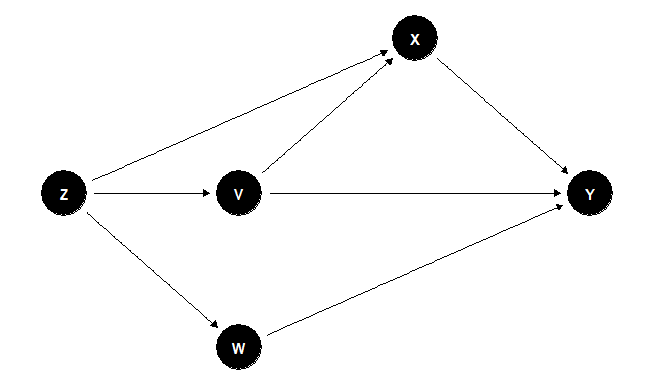
    Here is an example of the use of back-door criterion with simulated data for the SCM defined in figure 3.

    The process has the following steps

       

        1. Plot of SCM
        2. Review all the possible paths between the variables of interest.
        3. Definition of set of variables we need to control for.
        4. Data simulation
        5. Compute the causal effects.

      https://gist.github.com/pmgflores/fd3d6fba6b4cee511c6cec27dfe06188

      References

      Kline, R. B. (2015). Principles and Practice of Structural Equation Modeling, Fourth Edition. Guilford Publications.

      Pearl, J. (2009). Causal inference in statistics: An overview. Statistics Surveys, 3, 96–146.

      Shalizi, C. R. (n.d.). Advanced Data Analysis from an Elementary Point of View

      For this criterion, we can find a set of variables \( M \) that mediate all causal influence of \( X \) on \( Y \), which means that all of the direct paths from \( X \) to \( Y \) pass through \( M \). If we can identify the effect of \( M \) on \( Y \) and of \( X \) on \( M \), then we can combine these to get the effect of \( X \) on \( Y \). The test for whether we can do this combination is the front-door criterion. We say that a set of variables \( M \) satisfies the front-door criterion if (1) \( M \) blocks all direct paths from \( X \) to \( Y \), (2) there are no unblocked back-door paths from \( X \) to \( Y \), and (3) \( X \) blocks all back-door paths from \( M \) to \( Y \). Figure 4 presents an SCM in which all the effect of \( X \) on \( Y \) is mediated by the effect of \( X \) on \( M \). With this configuration, we can obtain the effect of \( X \) on \( M \) the back-door is blocked by the collider \( Y \), and the effect of \( M \) on \( Y \) because we can block the back door controlling by \( X \) with these results, finally we can compute the effect of \( X \) on \( Y \)

      Figure 4

      3. Instrumental Variables

      This last technique will be analyzed in more detail in the next post, but here is the gist of it. The idea is to find a variable \( I \) which affects \( X \) and which only affects \( Y \) by influencing \( X \). If we can identify the effect of \( I \) on \( Y \) and of \( I \) on \( X \), then we can “factor” them to get the effect of \( X \) on \( Y \). (That is, I gives us variation in \( X \), which is independent of the common causes of \( X \) and \( Y \).) \( I \) is then an instrumental variable for the effect of \( X \) on \( Y \).

      In Figure 5, we can see that the instrument \( I \) allows us to obtain the effect of \( I \) in \( X \) directly; then, we also can compute the effect of \( I \) on \( Y \) through \( X \) because the path \( I \rightarrow X \leftarrow U \rightarrow Y \) is blocked by the collider \( X \). With these results, it should be possible to “factor” the effect of \( X \) on \( Y \)

      Figure 5

      Limitations

      The main assumption of an SCM is that models must be created based on theoretical grounds. By combining models, structural equations, and observational data, researchers should be able to draw causal conclusions as long as they defend the logic of their assumptions. However, causal claims seem to be avoided by researchers since structural equations in SEM became an issue of the model adjustment than the theoretical implications behind it. Data can give researchers estimates but it cannot tell the reason why for those measures.

      A Back-door Example

      Here is an example of the use of back-door criterion with simulated data for the SCM defined in figure 3.

      The process has the following steps

         

          1. Plot of SCM
          2. Review all the possible paths between the variables of interest.
          3. Definition of set of variables we need to control for.
          4. Data simulation
          5. Compute the causal effects.

        https://gist.github.com/pmgflores/fd3d6fba6b4cee511c6cec27dfe06188

        References

        Kline, R. B. (2015). Principles and Practice of Structural Equation Modeling, Fourth Edition. Guilford Publications.

        Pearl, J. (2009). Causal inference in statistics: An overview. Statistics Surveys, 3, 96–146.

        Shalizi, C. R. (n.d.). Advanced Data Analysis from an Elementary Point of View

        For this criterion, we can find a set of variables \( M \) that mediate all causal influence of \( X \) on \( Y \), which means that all of the direct paths from \( X \) to \( Y \) pass through \( M \). If we can identify the effect of \( M \) on \( Y \) and of \( X \) on \( M \), then we can combine these to get the effect of \( X \) on \( Y \). The test for whether we can do this combination is the front-door criterion. We say that a set of variables \( M \) satisfies the front-door criterion if (1) \( M \) blocks all direct paths from \( X \) to \( Y \), (2) there are no unblocked back-door paths from \( X \) to \( Y \), and (3) \( X \) blocks all back-door paths from \( M \) to \( Y \). Figure 4 presents an SCM in which all the effect of \( X \) on \( Y \) is mediated by the effect of \( X \) on \( M \). With this configuration, we can obtain the effect of \( X \) on \( M \) the back-door is blocked by the collider \( Y \), and the effect of \( M \) on \( Y \) because we can block the back door controlling by \( X \) with these results, finally we can compute the effect of \( X \) on \( Y \)

        Figure 4

        3. Instrumental Variables

        This last technique will be analyzed in more detail in the next post, but here is the gist of it. The idea is to find a variable \( I \) which affects \( X \) and which only affects \( Y \) by influencing \( X \). If we can identify the effect of \( I \) on \( Y \) and of \( I \) on \( X \), then we can “factor” them to get the effect of \( X \) on \( Y \). (That is, I gives us variation in \( X \), which is independent of the common causes of \( X \) and \( Y \).) \( I \) is then an instrumental variable for the effect of \( X \) on \( Y \).

        In Figure 5, we can see that the instrument \( I \) allows us to obtain the effect of \( I \) in \( X \) directly; then, we also can compute the effect of \( I \) on \( Y \) through \( X \) because the path \( I \rightarrow X \leftarrow U \rightarrow Y \) is blocked by the collider \( X \). With these results, it should be possible to “factor” the effect of \( X \) on \( Y \)

        Figure 5

        Limitations

        The main assumption of an SCM is that models must be created based on theoretical grounds. By combining models, structural equations, and observational data, researchers should be able to draw causal conclusions as long as they defend the logic of their assumptions. However, causal claims seem to be avoided by researchers since structural equations in SEM became an issue of the model adjustment than the theoretical implications behind it. Data can give researchers estimates but it cannot tell the reason why for those measures.

        A Back-door Example

        Here is an example of the use of back-door criterion with simulated data for the SCM defined in figure 3.

        The process has the following steps

           

            1. Plot of SCM
            2. Review all the possible paths between the variables of interest.
            3. Definition of set of variables we need to control for.
            4. Data simulation
            5. Compute the causal effects.

          https://gist.github.com/pmgflores/fd3d6fba6b4cee511c6cec27dfe06188

          References

          Kline, R. B. (2015). Principles and Practice of Structural Equation Modeling, Fourth Edition. Guilford Publications.

          Pearl, J. (2009). Causal inference in statistics: An overview. Statistics Surveys, 3, 96–146.

          Shalizi, C. R. (n.d.). Advanced Data Analysis from an Elementary Point of View

            1. Chain: \((X \rightarrow W \rightarrow Y)\) where represents a mediator.
            2. Fork: \((X \leftarrow W \rightarrow Y)\) where \(W\) represents a common cause or confounder.
            3. Collider \((X \rightarrow W \leftarrow Y)\)

            These blocks have implications for the covariate selection in regression analysis. Given a causal model, it is appropriate to control for the confounders to avoid confounder bias; inadvertently controlling for a mediator might eliminate some or all the causal effects in the chain, and controlling for a collider can lead to collider bias, which induces spurious association.

            I want to illustrate an example to clarify the elements I have introduced so far. You might remember the example in the Granger Causality post trying to predict if Xavier’s emotional expressions help predict Yvonne’s emotions. Let’s make some changes to the same example to use it with a SCM. Now, we are interested in the causal effect of the emotions expressed by Xavier on the emotions posted by Yvonne later, represented in Figure 2. You might think that it is not possible to make that argument because other variables could affect Xavier and Yvonne’s emotions, such as the weather, but that is why this diagram includes the variable \(U\). This new variable represents all the Unobserved factors that generate confounding between the emotional expressions of Xavier and Yvonne. Assuming that, theoretically, this model is correct (which is a powerful claim), the representation establishes a causal mechanism that is different from the prediction I presented in the example of the Granger causality post. It is relevant to notice that the causal claim of the model should be based on theoretical grounds.

            Figure 2

            According to the model proposed in Figure 2, there are three variables: \( X \), which represents Xavier’s emotional expression, \( U \), showing the possible unobserved confounders such as the weather, the trending topics on the social media platform, etc., and the emotional expression of Yvonne \( Y \). Also, we can observe three causal relationships \( X \rightarrow Y \), \( U \rightarrow X \), and \( U \rightarrow Y \). This model tells us that Xavier’s emotions and unobserved variables ’cause’ the emotional expression of Yvonne, but also that the unobserved variables have a causal effect on Xavier’s emotions. The structure \( X \leftarrow U \rightarrow Y \) is a confounder between the variables Xavier and Yvonne, so if we want to obtain a correct causal effect of Xavier on Yvonne, it is needed to control for the unobserved variables. This example also helps to visualize that if we are interested in the causal effect of \( U \) on Yvonne, the variable Xavier acts as a mediator between them.

            Analysis

            Causal diagrams present the problem that noncausal paths can generate confounding. Therefore, causal claims would be wrong in that scenario. To correct this problem and decounfound two given variables of interest such as \( X \) and \( Y \), it is necessary to block every noncausal path between them without blocking or perturbing any causal paths. Because the previous task can be complicated, there are three main techniques to find the adequate set of controls to make the proper adjustments and calculate causal effects (Shalizi, forthcoming).

            1. Back-door criterion

            In an SCM, if we can condition on an intelligently chosen set of covariates \( S \), which block all the indirect paths from \( X \) to \( Y \) but leave all the direct paths open it is possible to compute the causal effect from \( X \) to \( Y \). We apply the back-door criterion to see whether a candidate set of controls \( S\) is adequate. A back-door path is a path between \( X \) and \( Y \) that starts with an arrow into \( X \); they are also called indirect paths. These paths generate confounding effects by creating a non-causal channel along which information flows. A set of control variables \( S \) satisfies the back-door criterion if (1) \( S \) blocks all back-door paths between \( X \) and \( Y \), and (2) no node in \( S \) is caused by \( X \).

            The example in Figure 3 shows four different back-door paths between \( X \) and \( Y \). (1) \( X \leftarrow V \rightarrow Y \), (2) \( X \leftarrow V \leftarrow Z \rightarrow W \rightarrow Y \), (3) \( X \leftarrow Z \rightarrow V \rightarrow Y \), and (4) \( X \leftarrow Z \rightarrow W \rightarrow Y \).

            Figure 3

            2. Front-door criterion

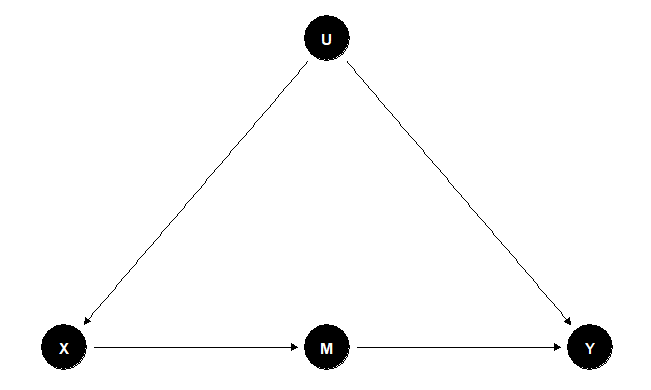
            For this criterion, we can find a set of variables \( M \) that mediate all causal influence of \( X \) on \( Y \), which means that all of the direct paths from \( X \) to \( Y \) pass through \( M \). If we can identify the effect of \( M \) on \( Y \) and of \( X \) on \( M \), then we can combine these to get the effect of \( X \) on \( Y \). The test for whether we can do this combination is the front-door criterion. We say that a set of variables \( M \) satisfies the front-door criterion if (1) \( M \) blocks all direct paths from \( X \) to \( Y \), (2) there are no unblocked back-door paths from \( X \) to \( Y \), and (3) \( X \) blocks all back-door paths from \( M \) to \( Y \). Figure 4 presents an SCM in which all the effect of \( X \) on \( Y \) is mediated by the effect of \( X \) on \( M \). With this configuration, we can obtain the effect of \( X \) on \( M \) the back-door is blocked by the collider \( Y \), and the effect of \( M \) on \( Y \) because we can block the back door controlling by \( X \) with these results, finally we can compute the effect of \( X \) on \( Y \)

            Figure 4

            3. Instrumental Variables

            This last technique will be analyzed in more detail in the next post, but here is the gist of it. The idea is to find a variable \( I \) which affects \( X \) and which only affects \( Y \) by influencing \( X \). If we can identify the effect of \( I \) on \( Y \) and of \( I \) on \( X \), then we can “factor” them to get the effect of \( X \) on \( Y \). (That is, I gives us variation in \( X \), which is independent of the common causes of \( X \) and \( Y \).) \( I \) is then an instrumental variable for the effect of \( X \) on \( Y \).

            In Figure 5, we can see that the instrument \( I \) allows us to obtain the effect of \( I \) in \( X \) directly; then, we also can compute the effect of \( I \) on \( Y \) through \( X \) because the path \( I \rightarrow X \leftarrow U \rightarrow Y \) is blocked by the collider \( X \). With these results, it should be possible to “factor” the effect of \( X \) on \( Y \)

            Figure 5

            Limitations

            The main assumption of an SCM is that models must be created based on theoretical grounds. By combining models, structural equations, and observational data, researchers should be able to draw causal conclusions as long as they defend the logic of their assumptions. However, causal claims seem to be avoided by researchers since structural equations in SEM became an issue of the model adjustment than the theoretical implications behind it. Data can give researchers estimates but it cannot tell the reason why for those measures.

            A Back-door Example

            Here is an example of the use of back-door criterion with simulated data for the SCM defined in figure 3.

            The process has the following steps

               

                1. Plot of SCM
                2. Review all the possible paths between the variables of interest.
                3. Definition of set of variables we need to control for.
                4. Data simulation
                5. Compute the causal effects.

              https://gist.github.com/pmgflores/fd3d6fba6b4cee511c6cec27dfe06188

              References

              Kline, R. B. (2015). Principles and Practice of Structural Equation Modeling, Fourth Edition. Guilford Publications.

              Pearl, J. (2009). Causal inference in statistics: An overview. Statistics Surveys, 3, 96–146.

              Shalizi, C. R. (n.d.). Advanced Data Analysis from an Elementary Point of View