Granger Causality
This is the first of a series of posts where I would like to introduce methods that can be useful when we are interested in research questions about cause and effect in social sciences. The method I picked, to begin with, is called Granger Causality, which might be the best-known (so-called) ‘causal method’ in the social sciences, last but not least because it is Nobel-Prize crowned.
Causality and Granger
In the 1960s, Professor Clive Granger was interested in pairs of interrelated stochastic processes. Moreover, he wanted to know if the relationship between processes could be broken down into a pair of one-way relationships. By reviewing the idea of Norbert Wiener (1956), who proposed that prediction theory could be used to define causality between time series, Granger started a discussion of a practical adaptation for this concept, which was finally coined as Granger causality. As we shall see, this term is a misnomer, as “Granger predictability” might be a better term; even Granger himself acknowledged during his Nobel lecture (2003) that he didn’t know that many people had fixed ideas about causation. However, because of his pragmatic definition, Granger got plenty of citations, but, in his own words, “many ridiculous papers appeared” as well. In Figure 1, we can observe that Granger causality is basically prediction; the information contained in one time series allows the observer to predict, with a time-lag, the behavior of another time series of interest. The time-lag is what provides theoretical justification for directionality in the correlation between both variables. However, note that this does not assure that some other (unobserved) variable might have been the true “cause” of what is observed, and the observed variable is simply a confounder.
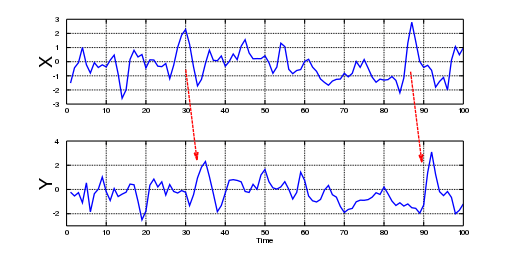
Figure 1
Before going into the formal details of the method, I would like to present the logic of Granger causality with an example. Let’s say that we are interested in predicting Yvonne’s emotional expression on social media tomorrow. An initial approach would be to think that Yvonne’s emotions will be based on how she is feeling today, yesterday, and the day before yesterday, so we are looking at the historical information of Yvonne posting online; in other words, at the time series of Yvonne’s emotions. We can also think about another approach. It might be that Yvonne’s emotions are not only based on her own history, but the content she posts online also depends on the online emotional expression of her best friend, Xavier. In this case, the new explanation examines the time series of Yvonne and Xavier’s emotions. If, after comparing these two approaches, we conclude that the latter is better because it gives us a more accurate prediction of Yvonne’s emotional expression, then we conclude that the emotions of Xavier “Granger causes” the emotions of Yvonne. Of course, from this toy example, you can already see all the problems associated with the term “causality,” as nothing assures that neither her own expressions nor Xavier’s emotions “caused” anything associated with Yvonne’s future posts. But semantics aside, let’s have a closer look at what Granger actually showed about the “co-integration” of two time series (which was the actual title of his Nobel Prize). In Figure 2 (top), you can see a representation in which only Yvonnepast affects Yvonnefuture, whereas the bottom part shows the alternative option, including Xavierpast affecting Yvonnefuture.
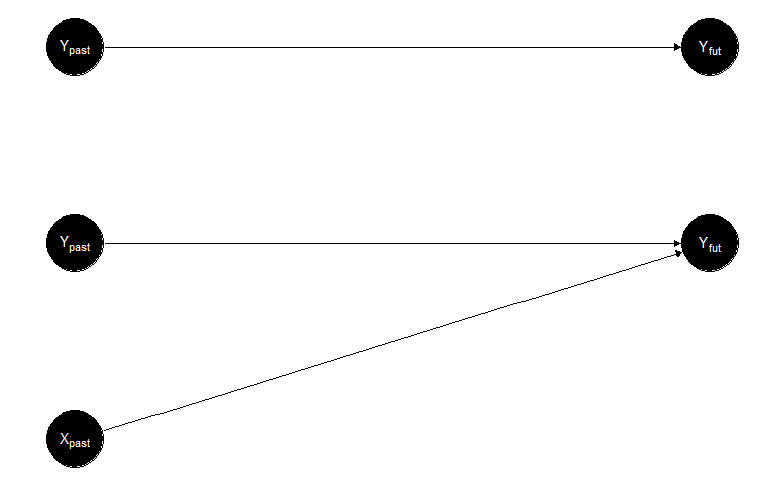
Figure 2
The mathematical formulation of Granger causality could be represented as follows. Let’s suppose that we have two time series \( X_t \) and \( Y_t \), if we are trying to predict \( Y_{t+1} \), we can do it only using the past terms of \( Y_t \) so its future depends only on its own past, or we can use both time series \( X_t \) and \( Y_t \) to make the prediction. If the later prediction considering a relationship between the two time series is significantly better, then it is possible to argue that the past of \( X_t \) contains valuable information to predict \( Y_{t+1} \); therefore, there is a one-way relationship from \( X_t \) to \( Y_t \). In this case, the conclusion is \( X_t \) “Granger causes” \( Y_t \). This conclusion can be made because the analysis rests on the proposition of two funding axioms made by Granger (1980):
- The cause happens before its effect.
- The cause has unique information about the future values of its effect.
It is important to point out that the term causality can be a bit misleading. Granger causality shows that the change in the temporal evolution of one variable precedes the change of values on another. Since time proceeds only in one direction (as far as humans can perceive), the time delay establishes directionality or better time-bound predictability. Still, it is mute on the more profound question of the mechanisms of causality. People solve this debate by using the term “Granger causality” to distinguish between this practical definition and causality.
Analysis
To make an analysis using Granger causality, we need to be familiar with linear autoregressive models, which is a fancy name for a linear method used to predict future behavior based on past information of the same variable. A typical mathematical representation of an autoregressive model with one time-lag would be:
\[ Y(t) = \alpha_1 Y(t-1) + error_1 (t) \tag{1} \]
Where \( \alpha \) represents the variable’s coefficient with one time-lag and the \( error_1 \) has a distribution with mean \( 0 \) and variance \( \sigma \).
As I mentioned earlier, the application of Granger causality compares two different models, one containing information from only one variable and the other from two. The model in (1) includes information on \( Y \) only, so we need a model with information about \( Y \) and another variable, which I will call \( X \), to proceed with the Granger causality analysis.
\[ Y(t) = \alpha_1 Y(t-1) + \beta_1 X(t-1) + error_2 (t) \tag{2} \]
Where \( \alpha \) represents the coefficient of the variable \( Y \) with one time-lag, \( \beta \) is the coefficient of the variable \( X \) with one time-lag, and the \( error_2 \) has a distribution with mean \( 0 \) and variance \( \sigma \).
Finally, once we have the models described in (1) and (2), a F-test is performed with the null hypothesis of \( Y(t) \) equals to model (1) against the alternative hypothesis of \( Y(t) \) equals to model (2). The final result allows us to evaluate if \( X \) Granger causes \( Y \) or not. We say that \( X \) Granger causes \( Y \) if we reject the null hypothesis.
The previous formulation presents the case when we include only one time-lag of the variables under study in the models. You might be asking what is the formulation for the general case. Using the sum notation, we can extend models (1) and (2) as follows:
\[ Y(t) = \sum_{j=1}^p \alpha_j Y(t-j) + error_1 (t) \tag{3} \]
\[ Y(t) = \sum_{j=1}^p \alpha_j Y(t-j) + \sum_{j=1}^p \beta_j X(t-j) + error_2 (t) \tag{4} \]
The same as the previous model in (3) and (4) \( \alpha_j \) and \( \beta_j \) are the coefficients of the model, \( error_1 \) and \( error_2 \) have a distribution with mean \( 0 \) and variance \( \sigma \), but there is a new element \( p \). Here \( p \) represents the maximum number of lagged observations included in the model. The selection of an appropriate number of lags \( p \) is a crucial decision to make before performing the analysis; we can base this choice on statistical criteria for information such as FPE, AIC, HQIC, and BIC. These measures compare the inherent trade-off between model complexity and the model’s predictive power, following Occam’s insight that models should only be as complex as necessary. However, theoretical considerations are also important in selecting the final number of lags to be included in the model. Once the decision of the maximum lagged observations is made, we proceed in the same fashion previously described in the case of \( p=1 \) to conclude if \( Y \) Granger causes \( X \).
Limitations
The study of Granger causality was initially designed for linear equations. There are extensions to nonlinear cases nowadays, but those extensions can be more challenging to understand and use. Moreover, their statistical meaning is less comprehended. Among the extensions, we can find approaches that divide the global nonlinear data into smaller locally linear neighborhoods (Freiwald et al., 1999) or the use of a radial basis function method to perform global nonlinear regression (Ancona et al., 2004)
Another limitation is that one of the assumptions of Granger causality requires that the time series be stationary, which means that their mean and variance should remain constant over time. Non-stationary time series can be transformed into stationary ones using the differentiation method. Additionally, assuming that short windows of non-stationary data produce locally stationary signals, it is possible to perform the analysis in such windows (Hesse et al., 2003).
A Granger Causality Application
As a student in the field of Communication, one of my interests is the study of the information dynamics that people create on social media. In this section, I want to share an application of Granger causality I have worked on.
For this example, the objective is to analyze if there is a relationship between online communicated emotions in the aftermath of a natural disaster. The approach seeks to understand if the emotions expressed after a tragic event follow a pattern in which it is possible to predict the appearance of some emotions based on the previous expression of other emotions. For example, after an earthquake, people express fear initially, but once time passes, the expression of emotion changes to sadness, so we would like to know if the initial information about fear helps to predict the later appearance of sadness. In this case, we collected data from Twitter in the aftermath of the earthquake in Southern California on July 5, 2019. To assess the emotion, each tweet was processed using the Natural Language Understanding tool provided by IBM Watson. This tool analyzes the text to assign a value from 0 to 1 for the presence of five emotions: sadness, anger, fear, disgust, and joy.
The procedure has the following steps:
- Check stationarity: We upload the data and check the stationarity of the time series.
- Stationarity correction: If required, we transform the time series to make them stationary.
- Lag selection: We selected the maximum lag for the analysis based on statistical and theoretical criteria.
- VAR analysis: We conduct an initial multivariate analysis to identify predictive relationships between the five emotions studied.
- Granger causality: Once we identify the predictive relationship between pairs of emotions, we conduct the analysis to determine if those relationships are Granger causal.
First we load and take a look at the data. The time series areconstructed as the average of the emotions expressed on Twitter in timeslots of five minutes during the 24 hours after the earthquake,therefore, every time series has 288 values.
#Set directorysetwd("C:\\Your directory")#Import the DDBB to be analyzedemotions <- read.csv("earthquakedata.csv", header = TRUE)#Plot of the time seriests.plot(emotions, col=c("cornflowerblue", "blue", "blue4","darkgoldenrod1","darkgoldenrod4" ), ylim=c(0,0.3))title(main = "Time series Southern California Earthquake", cex.main=1.5)legend("topright", legend = c("Sadness", "Anger", "Fear", "Disgust", "Joy"), cex = 1.0, bty="n", col = c("cornflowerblue", "blue", "blue4","darkgoldenrod1","darkgoldenrod4" ),lwd = 2)Step 1
To use Granger causality correctly we need to check if the time serieswe use are stationary. For that purpose we use the Augmented DickeyFuller (ADF) and KPSS tests. In the case of ADF with a p-value smallerthan .05 we can say that a time series is stationary while for KPSS weneed a p-value greater than .05
######################### Stationarity test ##########################We load the package tseries which contains the ADF and KPSS testslibrary("tseries")adf.test(emotions$sadness)## Warning in adf.test(emotions$sadness): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: emotions$sadness## Dickey-Fuller = -4.5096, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(emotions$anger)## Warning in adf.test(emotions$anger): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: emotions$anger## Dickey-Fuller = -5.2468, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(emotions$fear)## Warning in adf.test(emotions$fear): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: emotions$fear## Dickey-Fuller = -4.5921, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(emotions$disgust)## Warning in adf.test(emotions$disgust): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: emotions$disgust## Dickey-Fuller = -6.492, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(emotions$joy)## Warning in adf.test(emotions$joy): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: emotions$joy## Dickey-Fuller = -5.4876, Lag order = 6, p-value = 0.01## alternative hypothesis: stationarykpss.test(emotions$sadness)## ## KPSS Test for Level Stationarity## ## data: emotions$sadness## KPSS Level = 0.48228, Truncation lag parameter = 5, p-value = 0.04566kpss.test(emotions$anger)## Warning in kpss.test(emotions$anger): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: emotions$anger## KPSS Level = 0.33252, Truncation lag parameter = 5, p-value = 0.1kpss.test(emotions$fear)## Warning in kpss.test(emotions$fear): p-value smaller than printed p-value## ## KPSS Test for Level Stationarity## ## data: emotions$fear## KPSS Level = 2.0727, Truncation lag parameter = 5, p-value = 0.01kpss.test(emotions$disgust)## Warning in kpss.test(emotions$disgust): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: emotions$disgust## KPSS Level = 0.13877, Truncation lag parameter = 5, p-value = 0.1kpss.test(emotions$joy)## Warning in kpss.test(emotions$joy): p-value smaller than printed p-value## ## KPSS Test for Level Stationarity## ## data: emotions$joy## KPSS Level = 3.1366, Truncation lag parameter = 5, p-value = 0.01Step 2
From the previous results it is possible to notice that ADF and KPSSdon’t agree in all the results. Moreover sadness, fear, and joy arenot stationary for KPSS test. To proceed with the analysis we still needto transform the data in stationary time series. The transformation weuse is the differentiation of all the time series to keep theconsistency of the data then we analyze again if the transformed data isstationary.
######################################### Stationarity of first differences ##########################################Transformation of time seriesd_sadness <- diff(emotions$sadness)d_anger <- diff(emotions$anger)d_fear <- diff(emotions$fear)d_disgust <- diff(emotions$disgust)d_joy <- diff(emotions$joy)#New dataframe with the times series differentiatedd_emotions <- as.data.frame(cbind(d_sadness, d_anger, d_fear, d_disgust, d_joy))#Perform stationarity tests for transformed time seriesadf.test(d_emotions$d_sadness)## Warning in adf.test(d_emotions$d_sadness): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: d_emotions$d_sadness## Dickey-Fuller = -10.683, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(d_emotions$d_anger)## Warning in adf.test(d_emotions$d_anger): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: d_emotions$d_anger## Dickey-Fuller = -10.585, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(d_emotions$d_fear)## Warning in adf.test(d_emotions$d_fear): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: d_emotions$d_fear## Dickey-Fuller = -10.255, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(d_emotions$d_disgust)## Warning in adf.test(d_emotions$d_disgust): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: d_emotions$d_disgust## Dickey-Fuller = -10.456, Lag order = 6, p-value = 0.01## alternative hypothesis: stationaryadf.test(d_emotions$d_joy)## Warning in adf.test(d_emotions$d_joy): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: d_emotions$d_joy## Dickey-Fuller = -10.625, Lag order = 6, p-value = 0.01## alternative hypothesis: stationarykpss.test(d_emotions$d_sadness)## Warning in kpss.test(d_emotions$d_sadness): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: d_emotions$d_sadness## KPSS Level = 0.017846, Truncation lag parameter = 5, p-value = 0.1kpss.test(d_emotions$d_anger)## Warning in kpss.test(d_emotions$d_anger): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: d_emotions$d_anger## KPSS Level = 0.11013, Truncation lag parameter = 5, p-value = 0.1kpss.test(d_emotions$d_fear)## Warning in kpss.test(d_emotions$d_fear): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: d_emotions$d_fear## KPSS Level = 0.036515, Truncation lag parameter = 5, p-value = 0.1kpss.test(d_emotions$d_disgust)## Warning in kpss.test(d_emotions$d_disgust): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: d_emotions$d_disgust## KPSS Level = 0.03343, Truncation lag parameter = 5, p-value = 0.1kpss.test(d_emotions$d_joy)## Warning in kpss.test(d_emotions$d_joy): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: d_emotions$d_joy## KPSS Level = 0.011566, Truncation lag parameter = 5, p-value = 0.1Step 3
Once all the time series comply with the requirement of stationarity weneed to select the appropiate number of lags for the analysis.
##################### Lag selection ######################We use the tsDyn package for the analysisvar_lag <- tsDyn::lags.select(d_emotions)var_lag## Best AIC: lag= 10 ## Best BIC: lag= 2 ## Best HQ : lag= 4From the previous result we incorporate a lag of 2 in the analysis basedon BIC criterion. The reason to select BIC is that this criterion triesto find the true model among the set of candidates plus from thestructure of the data it makes sense to include tweets from two timeslots in the past which represents 10 minutes instead of 20 or 50minutes which are the options of HQ and AIC criterion respectively.
Step 4
It was mentioned that our interest was to find if it was possible topredict the appearence of one emotion based in the previous expressionof other emotions. Following a data driven approach we used a methodcalled Vector Auto Regresive (VAR) analysis to identify what emotionsmake predictions on others. The use of the VAR method allow us toincorporate a multivariate analysis for each emotion. For example, wetry to predict sadness with information from the past of sadness itselfplus anger, fear, disgust, and joy in the same model, then the resulttell us what emotions are significant for the prediction of sadness.Let’s assume that in this case the only significant emotion to predictsadness is anger but because of the multivariate nature of the VARanalysis it is hard to make an interpretation of the relationshipbetween them. At this point we move forward to make a Granger causalanalysis between sadness and anger that can be interpreted consideringwhat we have learned in this post.
#################### VAR analysis #####################We load vars package to perform the analysislibrary("vars")var_results <- VAR(d_emotions, p = 2) #p=2 refers to the maximum lag selectedsummary(var_results)## ## VAR Estimation Results:## ========================= ## Endogenous variables: d_sadness, d_anger, d_fear, d_disgust, d_joy ## Deterministic variables: const ## Sample size: 285 ## Log Likelihood: 3641.218 ## Roots of the characteristic polynomial:## 0.6317 0.6317 0.6183 0.6183 0.585 0.585 0.5751 0.5751 0.3746 0.3746## Call:## VAR(y = d_emotions, p = 2)## ## ## Estimation results for equation d_sadness: ## ========================================== ## d_sadness = d_sadness.l1 + d_anger.l1 + d_fear.l1 + d_disgust.l1 + d_joy.l1 + d_sadness.l2 + d_anger.l2 + d_fear.l2 + d_disgust.l2 + d_joy.l2 + const ## ## Estimate Std. Error t value Pr(>|t|) ## d_sadness.l1 -0.6953898 0.0585405 -11.879 < 2e-16 ***## d_anger.l1 0.0347770 0.0858959 0.405 0.6859 ## d_fear.l1 -0.0470720 0.0724411 -0.650 0.5164 ## d_disgust.l1 0.1624978 0.1206383 1.347 0.1791 ## d_joy.l1 -0.0949055 0.0564832 -1.680 0.0940 . ## d_sadness.l2 -0.3730392 0.0585910 -6.367 8.1e-10 ***## d_anger.l2 0.0731065 0.0849923 0.860 0.3905 ## d_fear.l2 -0.1260265 0.0725353 -1.737 0.0834 . ## d_disgust.l2 -0.0638156 0.1213525 -0.526 0.5994 ## d_joy.l2 -0.0795697 0.0570315 -1.395 0.1641 ## const 0.0001768 0.0014627 0.121 0.9039 ## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## ## Residual standard error: 0.02467 on 274 degrees of freedom## Multiple R-Squared: 0.3689, Adjusted R-squared: 0.3459 ## F-statistic: 16.02 on 10 and 274 DF, p-value: < 2.2e-16 ## ## ## Estimation results for equation d_anger: ## ======================================== ## d_anger = d_sadness.l1 + d_anger.l1 + d_fear.l1 + d_disgust.l1 + d_joy.l1 + d_sadness.l2 + d_anger.l2 + d_fear.l2 + d_disgust.l2 + d_joy.l2 + const ## ## Estimate Std. Error t value Pr(>|t|) ## d_sadness.l1 -0.0557819 0.0427400 -1.305 0.192939 ## d_anger.l1 -0.4504857 0.0627119 -7.183 6.43e-12 ***## d_fear.l1 0.0974610 0.0528887 1.843 0.066445 . ## d_disgust.l1 0.1366864 0.0880771 1.552 0.121842 ## d_joy.l1 0.0700432 0.0412380 1.699 0.090546 . ## d_sadness.l2 -0.0408431 0.0427769 -0.955 0.340523 ## d_anger.l2 -0.2173795 0.0620522 -3.503 0.000537 ***## d_fear.l2 0.0133412 0.0529575 0.252 0.801289 ## d_disgust.l2 -0.0451519 0.0885986 -0.510 0.610726 ## d_joy.l2 -0.0300140 0.0416383 -0.721 0.471630 ## const -0.0004434 0.0010679 -0.415 0.678298 ## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## ## Residual standard error: 0.01801 on 274 degrees of freedom## Multiple R-Squared: 0.2279, Adjusted R-squared: 0.1997 ## F-statistic: 8.088 on 10 and 274 DF, p-value: 1.922e-11 ## ## ## Estimation results for equation d_fear: ## ======================================= ## d_fear = d_sadness.l1 + d_anger.l1 + d_fear.l1 + d_disgust.l1 + d_joy.l1 + d_sadness.l2 + d_anger.l2 + d_fear.l2 + d_disgust.l2 + d_joy.l2 + const ## ## Estimate Std. Error t value Pr(>|t|) ## d_sadness.l1 -1.168e-02 5.100e-02 -0.229 0.8190 ## d_anger.l1 1.222e-01 7.483e-02 1.633 0.1036 ## d_fear.l1 -5.181e-01 6.311e-02 -8.210 8.77e-15 ***## d_disgust.l1 3.388e-02 1.051e-01 0.322 0.7474 ## d_joy.l1 1.278e-02 4.921e-02 0.260 0.7953 ## d_sadness.l2 1.175e-01 5.104e-02 2.302 0.0221 * ## d_anger.l2 1.415e-02 7.404e-02 0.191 0.8485 ## d_fear.l2 -2.531e-01 6.319e-02 -4.006 7.96e-05 ***## d_disgust.l2 8.289e-02 1.057e-01 0.784 0.4337 ## d_joy.l2 -4.362e-02 4.968e-02 -0.878 0.3808 ## const -6.722e-05 1.274e-03 -0.053 0.9580 ## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## ## Residual standard error: 0.02149 on 274 degrees of freedom## Multiple R-Squared: 0.2594, Adjusted R-squared: 0.2324 ## F-statistic: 9.599 on 10 and 274 DF, p-value: 1.048e-13 ## ## ## Estimation results for equation d_disgust: ## ========================================== ## d_disgust = d_sadness.l1 + d_anger.l1 + d_fear.l1 + d_disgust.l1 + d_joy.l1 + d_sadness.l2 + d_anger.l2 + d_fear.l2 + d_disgust.l2 + d_joy.l2 + const ## ## Estimate Std. Error t value Pr(>|t|) ## d_sadness.l1 1.252e-02 2.911e-02 0.430 0.667 ## d_anger.l1 -2.278e-02 4.271e-02 -0.533 0.594 ## d_fear.l1 -4.157e-02 3.602e-02 -1.154 0.249 ## d_disgust.l1 -5.783e-01 5.999e-02 -9.639 < 2e-16 ***## d_joy.l1 3.125e-02 2.809e-02 1.113 0.267 ## d_sadness.l2 -1.456e-02 2.914e-02 -0.500 0.618 ## d_anger.l2 1.587e-02 4.226e-02 0.376 0.708 ## d_fear.l2 -3.213e-02 3.607e-02 -0.891 0.374 ## d_disgust.l2 -3.645e-01 6.035e-02 -6.041 4.99e-09 ***## d_joy.l2 7.515e-03 2.836e-02 0.265 0.791 ## const 4.957e-05 7.273e-04 0.068 0.946 ## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## ## Residual standard error: 0.01227 on 274 degrees of freedom## Multiple R-Squared: 0.295, Adjusted R-squared: 0.2692 ## F-statistic: 11.46 on 10 and 274 DF, p-value: < 2.2e-16 ## ## ## Estimation results for equation d_joy: ## ====================================== ## d_joy = d_sadness.l1 + d_anger.l1 + d_fear.l1 + d_disgust.l1 + d_joy.l1 + d_sadness.l2 + d_anger.l2 + d_fear.l2 + d_disgust.l2 + d_joy.l2 + const ## ## Estimate Std. Error t value Pr(>|t|) ## d_sadness.l1 0.1160292 0.0606994 1.912 0.056978 . ## d_anger.l1 0.0070177 0.0890635 0.079 0.937254 ## d_fear.l1 -0.0447704 0.0751125 -0.596 0.551637 ## d_disgust.l1 -0.2522966 0.1250871 -2.017 0.044674 * ## d_joy.l1 -0.6090107 0.0585661 -10.399 < 2e-16 ***## d_sadness.l2 0.1404621 0.0607517 2.312 0.021515 * ## d_anger.l2 -0.3321738 0.0881266 -3.769 0.000201 ***## d_fear.l2 -0.1014774 0.0752102 -1.349 0.178370 ## d_disgust.l2 -0.0672985 0.1258276 -0.535 0.593190 ## d_joy.l2 -0.3127464 0.0591347 -5.289 2.52e-07 ***## const -0.0003091 0.0015166 -0.204 0.838678 ## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1## ## ## Residual standard error: 0.02558 on 274 degrees of freedom## Multiple R-Squared: 0.3708, Adjusted R-squared: 0.3478 ## F-statistic: 16.15 on 10 and 274 DF, p-value: < 2.2e-16 ## ## ## ## Covariance matrix of residuals:## d_sadness d_anger d_fear d_disgust d_joy## d_sadness 6.087e-04 3.678e-05 1.031e-04 2.280e-05 -1.436e-04## d_anger 3.678e-05 3.245e-04 7.150e-05 3.134e-05 -1.338e-04## d_fear 1.031e-04 7.150e-05 4.619e-04 -4.951e-05 -6.023e-05## d_disgust 2.280e-05 3.134e-05 -4.951e-05 1.505e-04 -4.690e-06## d_joy -1.436e-04 -1.338e-04 -6.023e-05 -4.690e-06 6.544e-04## ## Correlation matrix of residuals:## d_sadness d_anger d_fear d_disgust d_joy## d_sadness 1.00000 0.08277 0.1945 0.07533 -0.22756## d_anger 0.08277 1.00000 0.1847 0.14180 -0.29041## d_fear 0.19448 0.18468 1.0000 -0.18776 -0.10954## d_disgust 0.07533 0.14180 -0.1878 1.00000 -0.01494## d_joy -0.22756 -0.29041 -0.1095 -0.01494 1.00000Step 5
Now that the VAR analysis help us to identify significant relationshipsbetween emotions. We procede to perform the Granger causal analysisbetween fear/sadness, joy/anger, joy/sadness, and joy/disgust.
############################################################ Revising significant relationships Granger causality #############################################################We perform all the pairwise granger causality analysisgrangertest(d_emotions$d_fear ~ d_emotions$d_sadness, order=2) #order=2 refers to the maximum lag selected ## Granger causality test## ## Model 1: d_emotions$d_fear ~ Lags(d_emotions$d_fear, 1:2) + Lags(d_emotions$d_sadness, 1:2)## Model 2: d_emotions$d_fear ~ Lags(d_emotions$d_fear, 1:2)## Res.Df Df F Pr(>F) ## 1 280 ## 2 282 -2 4.5796 0.01104 *## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1grangertest(d_emotions$d_sadness ~ d_emotions$d_fear, order=2)## Granger causality test## ## Model 1: d_emotions$d_sadness ~ Lags(d_emotions$d_sadness, 1:2) + Lags(d_emotions$d_fear, 1:2)## Model 2: d_emotions$d_sadness ~ Lags(d_emotions$d_sadness, 1:2)## Res.Df Df F Pr(>F)## 1 280 ## 2 282 -2 1.305 0.2728grangertest(d_emotions$d_joy ~ d_emotions$d_anger, order=2)## Granger causality test## ## Model 1: d_emotions$d_joy ~ Lags(d_emotions$d_joy, 1:2) + Lags(d_emotions$d_anger, 1:2)## Model 2: d_emotions$d_joy ~ Lags(d_emotions$d_joy, 1:2)## Res.Df Df F Pr(>F) ## 1 280 ## 2 282 -2 8.2868 0.0003188 ***## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1grangertest(d_emotions$d_anger ~ d_emotions$d_joy, order=2)## Granger causality test## ## Model 1: d_emotions$d_anger ~ Lags(d_emotions$d_anger, 1:2) + Lags(d_emotions$d_joy, 1:2)## Model 2: d_emotions$d_anger ~ Lags(d_emotions$d_anger, 1:2)## Res.Df Df F Pr(>F) ## 1 280 ## 2 282 -2 3.1286 0.04532 *## ---## Signif. codes: 0 "***" 0.001 "**" 0.01 "*" 0.05 "." 0.1 " " 1grangertest(d_emotions$d_joy ~ d_emotions$d_sadness, order=2)## Granger causality test## ## Model 1: d_emotions$d_joy ~ Lags(d_emotions$d_joy, 1:2) + Lags(d_emotions$d_sadness, 1:2)## Model 2: d_emotions$d_joy ~ Lags(d_emotions$d_joy, 1:2)## Res.Df Df F Pr(>F)## 1 280 ## 2 282 -2 2.0109 0.1358grangertest(d_emotions$d_sadness ~ d_emotions$d_joy, order=2)## Granger causality test## ## Model 1: d_emotions$d_sadness ~ Lags(d_emotions$d_sadness, 1:2) + Lags(d_emotions$d_joy, 1:2)## Model 2: d_emotions$d_sadness ~ Lags(d_emotions$d_sadness, 1:2)## Res.Df Df F Pr(>F)## 1 280 ## 2 282 -2 1.5771 0.2084grangertest(d_emotions$d_joy ~ d_emotions$d_disgust, order=2)## Granger causality test## ## Model 1: d_emotions$d_joy ~ Lags(d_emotions$d_joy, 1:2) + Lags(d_emotions$d_disgust, 1:2)## Model 2: d_emotions$d_joy ~ Lags(d_emotions$d_joy, 1:2)## Res.Df Df F Pr(>F)## 1 280 ## 2 282 -2 0.9428 0.3908grangertest(d_emotions$d_disgust ~ d_emotions$d_joy, order=2)## Granger causality test## ## Model 1: d_emotions$d_disgust ~ Lags(d_emotions$d_disgust, 1:2) + Lags(d_emotions$d_joy, 1:2)## Model 2: d_emotions$d_disgust ~ Lags(d_emotions$d_disgust, 1:2)## Res.Df Df F Pr(>F)## 1 280 ## 2 282 -2 0.9252 0.3977Results
From the final results of this example it is possible to appreciate thatSadness Granger causes Fear, which means that the expression of Sadnessin the aftermath of the Southern California earthquake predicts theexpression of Fear moments later. I also found that the relationshipbetween Anger and Joy is statistically significant in both ways whichcould mean that the expression of those emotions generate a loop betweenthem.The relationships between Joy and Sadness, and Joy and Disgust thatwere significant in the VAR analysis were not when I performed theGranger causality test.
References
Ancona, N., Marinazzo, D., & Stramaglia, S. (2004). Radial basis function approach to nonlinear Granger causality of time series. Physical Review E, 70(5), 056221. https://doi.org/10.1103/PhysRevE.70.056221
Brady, H. E. (2011). Causation and Explanation in Social Science. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199604456.013.0049
Freiwald, W. A., Valdes, P., Bosch, J., Biscay, R., Jimenez, J. C., Rodriguez, L. M., Rodriguez, V., Kreiter, A. K., & Singer, W. (1999). Testing non-linearity and directedness of interactions between neural groups in the macaque inferotemporal cortex. Journal of Neuroscience Methods, 94(1), 105–119. https://doi.org/10.1016/S0165-0270(99)00129-6
Granger, C. W. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society, 424–438.
Hesse, W., Möller, E., Arnold, M., & Schack, B. (2003). The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies. Journal of Neuroscience Methods, 124(1), 27–44. https://doi.org/10.1016/S0165-0270(02)00366-7
Wiener, N. (1956). The theory of prediction. Modern mathematics for engineers. New York, 165–190.
