ε-Machines
In the previous post of this series of methods related to causation and prediction, I want to introduce a new concept called ε-Machines. This is my first time using the term machines in these posts. Basically, we can think about machines as graphic representations of processes that show the possible states of a system and how it is possible to move from one state to another (transition).
The derivation and study of these types of machines is part of a field known as computational mechanics. According to Shalizi and Crutchfield (2001), “the goal of computational mechanics is to discern the patterns intrinsic to a process. That is, as much as possible, the goal is to let the process describe itself, on its own terms, without appealing to a priori assumptions about its structure.” It is important to notice that the same term also refers to something different concerning the use of computational methods to study events governed by the principle of mechanics. Knowing that there exist different interpretations for the same concept, we will focus on understanding how a process computes in this post.
Causal States, Transitions, and ε-Machines
To better explain the method, I am going to revise the concepts of causal states and transitions (state-to-state) that we need to understand what a causal state machine is.
A causal state of a process is defined as the set of histories that lead to the same prediction. For example, we want to predict Xavier’s emotional expression tomorrow. To make the prediction, we have two different pasts: \( \overleftarrow{s’} \) and \( \overleftarrow{s”} \). If the two pasts make the same prediction, we say that \( \overleftarrow{s’} \) and \( \overleftarrow{s”} \) have the same morph. Every causal state has a unique morph. Figure 1 shows an example of two causal states for the behavior of an automated bot on social media.
Figure 1
From Figure 1, we notice that determining causal states is not enough to define a process. For causal state machines, knowing the causal state at any given time and the next value of the observed process together determine a new causal state. In other words, a natural relation of succession exists among causal states. Moreover, given the current causal state, all the process’s possible next values have well-defined conditional probabilities. Formally, the transition probabilities between states \( T_{ij}^{(s)} \) is the probability of making a transition from state \( S_i \) to \( S_j \) while the next value of the process is \( s \).
To complete the diagram previously introduced in Figure 1, Figure 2 presents a causal state machine that describes a bot’s posting behavior (process) on social media. We can appreciate that the observed variable in the process is the bot’s mention (or not). The diagram lets us know what the next state will be given the current state and the value of the observed variable (mention). We also distinguish that this bot always posts when it is mentioned and is always still when not mentioned.
Figure 2
Now that we understand a little more about causal states, transition probabilities, and diagrams, let’s introduce ε-machines. By definition, the ε-machine of a process is the combination of the function that transforms histories into causal states with the transition probabilities among them.
Figure 3 shows the diagram of a toy example of an ε-machine. The idea is to try to predict Xavier’s emotional expression on social media based on the history of his posts on the same platform. So, the first step we must take is to collect Xavier’s past posts and measure their emotions. To make it easier, let’s say that the emotion measured is classified as positive or negative, with values 1 and 0, respectively. Therefore, we create a time series of values 0s and 1s. Using the structure of the time series, it is possible to determine the morphs present in the time series and the transition probabilities between them. As previously stated, the morphs determine the number of causal states present in the process. Once we have the causal states and the transitions, we can create the diagram for the ε-machine. The example clearly shows that ε-machines only use the information of one time series to predict a future state in the process. Essentially, we elaborate a model for the process based on autoregression but without the assumptions we use to develop ARMA or ARIMA models.
Figure 3
It is important to notice that ε-machines are predictive state machines that comply with three optimality theorems that capture all of the process’s properties: (1) prediction: a process’s ε-machine is its optimal predictor, (2) minimality: compared with other optimal predictors, a process´s ε-machine is its minimal representation, and (3) uniqueness: any minimal optimal predictor is equivalent to the ε-machine (Crutchfield, 2012).
Analysis
There are different methods to build ε-machines models from time series, such as topological methods (Crutchfield & Young, 1989), state-splitting (Shalizi et al., 2002; Shalizi & Shalizi, 2004), spectral decomposition, etc. However, the most didactical is the method of subtree reconstruction, which I will describe in more detail.
We are interested in obtaining the ε-machine of the process from observed empirical data. Let’s say that we collected the following data \( 110101011011110 \), and we decided to analyze the structure considering windows of length four. The first would be \( \underline{1101}01011011110 \), the second \( 1\underline{1010}1011011110 \), and so on until the last one \( 11010101101\underline{1110} \). If we draw all the possible windows in a tree structure, we will find out that some branches never occur like \( 0000 \), so we need to prune them, and the final tree that we obtain is reflected in Figure 4.
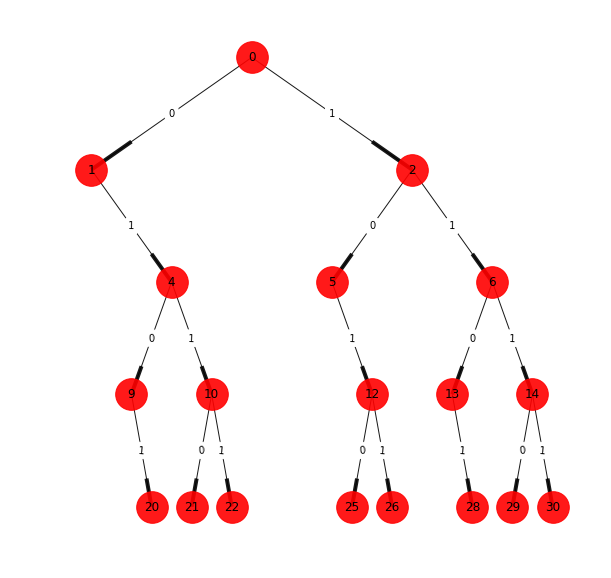
Figure 4
Now that the tree structure is defined, we look at the subtree structures that create the building blocks of the process. Considering branches of two steps into the future, it is possible to distinguish two different morphs, shown in Figures 5a and 5b. The morph of Figure 5a can be appreciated in the tree structure of Figure 4 starting in the nodes \( 0 \), \( 2 \), \( 4 \), and \( 6 \), while the morph 5b has starting nodes in \( 1 \) and \( 5 \).
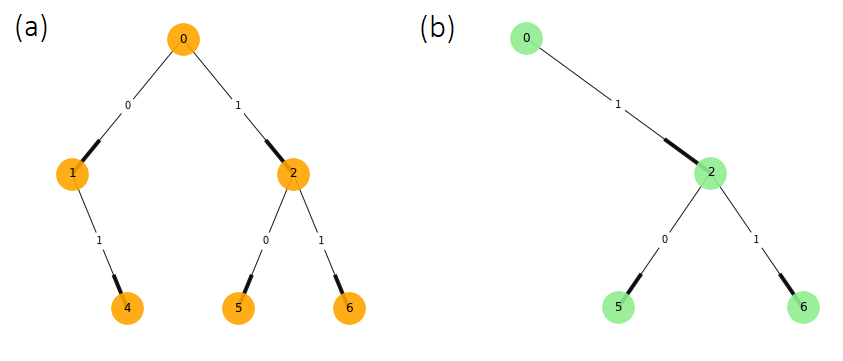
Figure 5
Using the previous morphs as the states of the process and the original tree structure, we can define the topological ε-machine shown in Figure 6 and its final diagram in Figure 7. This model produces strings of data that never contain two consecutive 0s.
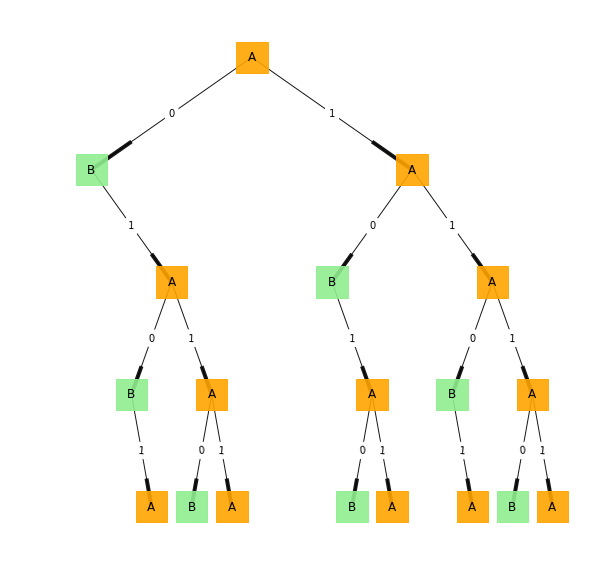
Figure 6
Figure 7
The final model we obtained represents the process topology, in other words, how the different components are arranged. However, it is important to recall that it does not say anything about the probabilities of the occurrences. By counting the frequency of the windows of length four, it is possible to provide an approximation of the transition probabilities shown in Figure 7. Now, each edge has two numbers following the format \( ed | p \) where \( ep \) represents the empirical data observed and \( p \) the probability of observing that specific data.
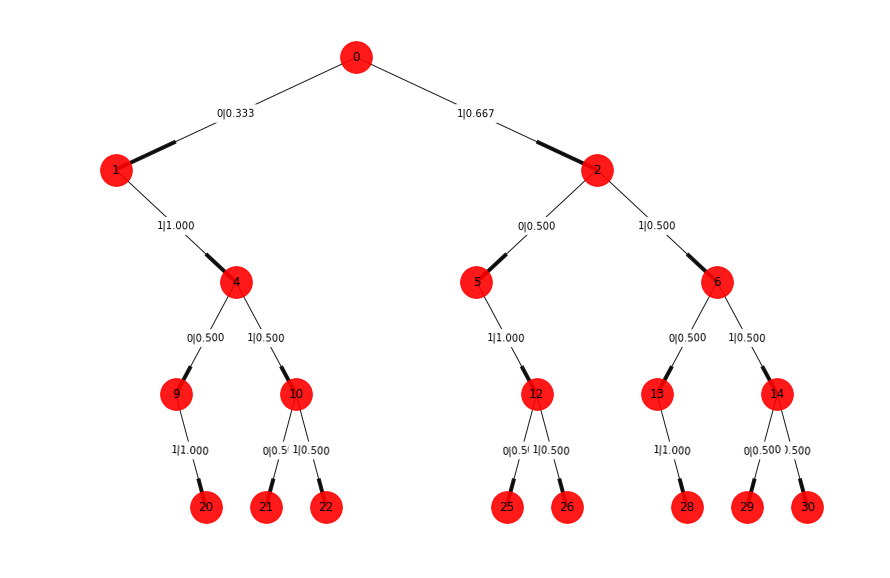
Figure 8
Taking a detailed look at Figure 8, we can now observe three different morphs because there is a slight difference in the probabilities between morphs A and C (see Figure 9). The new morph creates an initial state represented by the letter A in Figure 10.
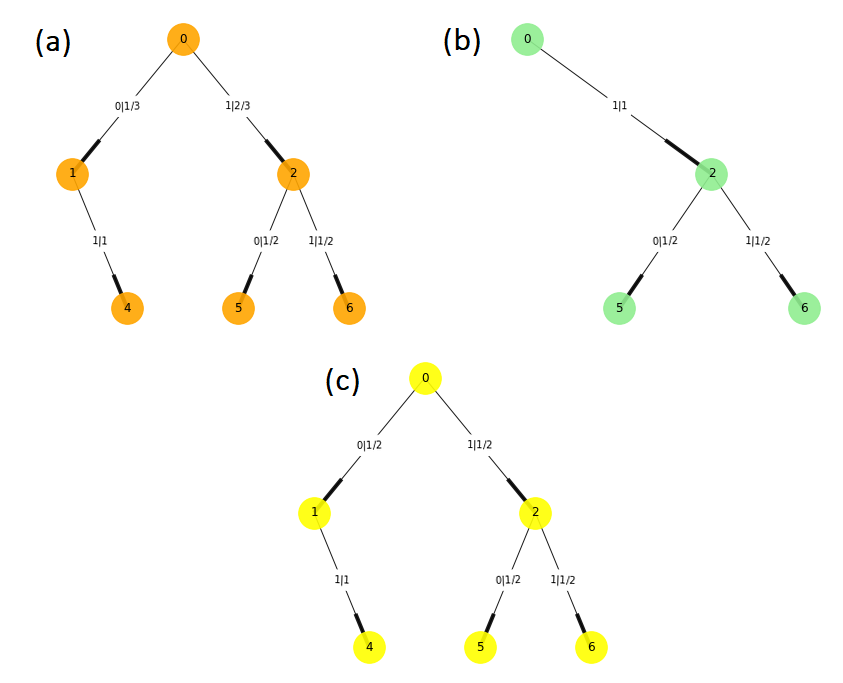
Figure 9
Figure 10
Another significant result of having a set of causal states and its probabilities for the ε-machines is that we can compute the information measures for the set of causal states \( S \). The entropy of the states of an ε-machine is called statistical complexity.
\[ H[S] = C_{\mu} \tag{1} \]
Using the definition, it is possible to affirm that “the statistical complexity of a state class is the average uncertainty (in bits) in the process’s current state. This, in turn, is the same as the average amount of memory (in bits) that the process appears to retain about the past” (Shalizi & Crutchfield, 2001). Simply, it is the amount of memory about the past required to predict the future.
Limitations
There are different limitations to the use of this tool; it is needed to observe processes that take on discrete values. The process also is discrete in the time variables.
Like the previous cases of transfer entropy and modes of information flow, the observed process must be stationary. The time series is pure, meaning it doesn’t have a spatial extent. Finally, the prediction is only based on the process’s past; we can’t add any other outside source of information.
References
Crutchfield, J. P. (2012). Between order and chaos. Nature Physics, 8(1), 17–24. https://doi.org/10.1038/nphys2190
Crutchfield, J. P., & Young, K. (1989). Inferring statistical complexity. Physical Review Letters, 63(2), 105–108. https://doi.org/10.1103/PhysRevLett.63.105
Shalizi, C. R., & Crutchfield, J. P. (2001). Computational mechanics: Pattern and prediction, structure and simplicity. Journal of Statistical Physics, 104(3), 817–879.
Shalizi, C. R., & Shalizi, K. L. (2004). Blind Construction of Optimal Nonlinear Recursive Predictors for Discrete Sequences. ArXiv:Cs/0406011. http://arxiv.org/abs/cs/0406011
Shalizi, C. R., Shalizi, K. L., & Crutchfield, J. P. (2002). An Algorithm for Pattern Discovery in Time Series. ArXiv:Cs/0210025. http://arxiv.org/abs/cs/0210025