Granger Causality

This is the first of a series of posts where I would like to share an introduction to methods that can be useful when we are interested in research questions about case and effects in social sciences. The method I picked, to begin with, is called Granger Causality, which might be the best-known (so-called) ‘causal method’ in the social sciences, last but not least because it is Nobel-Prize crowned.

Causality and Granger

In the 1960s Professor Clive Granger was interested in pairs of inter-related stochastic processes. Moreover, he wanted to know if the relationship between the processes could be broken down into a pair of one way relationship. By reviewing the idea of Norbert Wiener (1956) who proposed that prediction theory could be used to define causality between time series, Granger started a discussion of a practical adaptation for this concept which was finally coined as Granger causality. This term is actually a misnomer, as we shall see, as “Granger predictability” might be a better term, even Granger himself acknowledge during his Nobel lecture (2003) that he didn’t know that many people had fixed ideas about causation. However, because of his pragmatic definition Granger got plenty of citations but, in his own words, “many ridiculous papers appeared” as well. In figure 1 we can observe that Granger causality is basically prediction, the information contained in one time series allows the observer to predict, with a timelag, the behavior of another time series of interest. The timelag is what provides theoretical justification for directionality in the correlation between both variables. However, note that this does not assure that some other (unobserved) variable might have been the true “cause” of what is observed, and the observed variable is simply a confounder

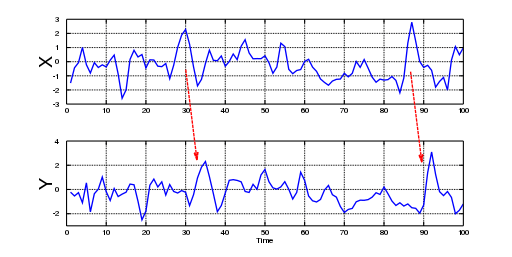
Figure 1

Before going into the formal details of the method, I would like to present the logic of Granger causality with an example. Let’s say that we are interested in predicting Yvonne’s emotional expression on social media tomorrow. An initial approach would be to think that Yvonne’s emotions will be based on how she is feeling today, yesterday, and the day before yesterday so we are looking at the historical information of Yvonne posting online, in other words, at the time series of Yvonne’s emotions. We can also think about another approach, it might be that Yvonne’s emotions are not only based on her own history, but the content she posts online also depends on the online emotional expression of her best friend, Xavier. In this case, the new explanation looks at the time series of Yvonne and Xavier’s emotions. If after making a comparison between these two approaches we conclude that the latter is better because it gives us a more accurate prediction of Yvonne’s emotional expression then we conclude that the emotions of Xavier “Granger-causes” the emotions of Yvonne. Of course, from this toy example you can already see all the problems associated with the term “causality”, as nothing assures that neither her own expressions, nor Xavier emotions “caused” anything associated with Yvonne’s future posts. But semantics aside, let’s have a closer look at what Granger actually showed about the “co-integration” of two timeseries (which was the actualy title of his Nobel Prize). In figure 2 (top) you can see a representation in which only Yvonne_past affects Yvonne_future, whereas, the bottom part of the figure shows the alternative option including Xavier_past affecting Yvonne_future.

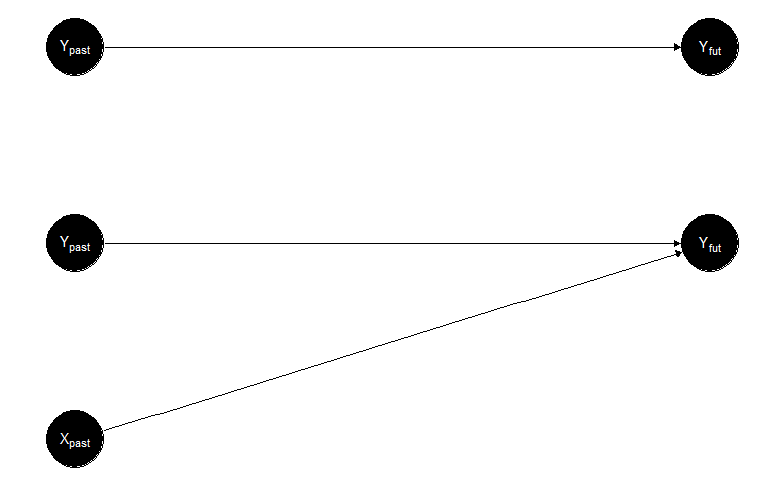
Figure 2

The mathematical formulation of Granger causality could be represented as follows. Let’s suppose that we have two time series $X_t$ and $Y_t$ if we are trying to predict $Y_{t+1}$ we can do it only using the past terms of $Y_t$ so its future depends only on its own past or, alternatively, we can use both time series $X_t$ and $Y_t$ to make the prediction. If the later prediction considering a relationship between the two time series is significantly better, then it is possible to argue that the past of $X_t$ contains valuable information to predict $Y_{t+1}$ , therefore, there is a one way relationship from $X_t$ to $Y_t$ . In this case the conclusion is $X_t$ “Granger causes” $Y_t$ . This conclusion can be made because the analysis rests in the proposition of two funding axioms made by Granger (1980):

The cause happens before its effect.
The cause has unique information about the future values of its effect.

It is important to point out that the term causality can be a bit misleading, Granger causality shows that the change in the temporal evolution on one variable precedes the change of values on another. Since time proceeds only in one direction (as far as human can perceive) the time delay establishes directionality, or better time-bound predictability, but it is mute on the deeper question of the mechanims of causality. People solves this important debate by using the term of “Granger causality” making a distinction between this practical definition and causality.

Analysis

To make an analysis using Granger causality we need to be familiar with linear autoregresive models, which is a fancy name for a linear method used to predict future behavior based on past information of the same variable. A typical mathematical representation of an autoregresive model with one timelag would be:

(1) $Y(t) = \alpha_1 Y(t-1) + error_1 (t)$

Where $\alpha$ represents the coefficient of the variable with one timelag and the $error_1$ has a distribution with mean $0$ and variance $\sigma$ .

As I mentioned earlier the application of Granger causality makes a comparison between two different models one of them containing information from only one variable and the other containing information of two. The model in (1) contains information about $Y$ only so we need a model with information about $Y$ and another variable, which I will call $X$ , to procede with the Granger causality analysis.

(2) $Y(t) = \alpha_1 Y(t-1) + \beta_1 X(t-1) + error_2 (t)$

Where $\alpha$ represents the coefficient of the variable $Y$ with one timelag, $\beta$ is the coefficient of the variable $X$ with one timelag and the $error_2$ has a distribution with mean $0$ and variance $\sigma$ .

Finally, once we have the models described in (1) and (2) a F-test is performed with the null hypothesis of $Y(t)$ equals to model (1) against the alternative hypothesis of $Y(t)$ equals to model (2). The final result allows to evaluate if $X$ Granger causes $Y$ or not. We say that $X$ Granger causes $Y$ if we reject the null hypothesis.

The previous formulation presents the case when we include only one timelag of the variables under study in the models. You might be asking what is the formulation for the general case. Using the sum notation we can extend models (1) and (2) as follows:

(3) $Y(t) = \sum_{j=1}^p \alpha_j Y(t-j) + error_1 (t)$

(4) $Y(t) = \sum_{j=1}^p \alpha_j Y(t-j) + \sum_{j=1}^p \beta_j X(t-j) + error_2 (t)$

The same as the previous model in (3) and (4) $\alpha_j$ and $\beta_j$ are the coefficients of the model, $error_1$ and $error_2$ have a distribution with mean $0$ and variance $\sigma$ , but there is a new element $p$ . Here $p$ represents the maximum number of lagged observations included in the model. The selection of an appropiate number of lags $p$ is an important decision to make before performing the analysis, we can base this choice in statistical criteria for information such as FPE, AIC, HQIC, and BIC. These are basically measures that compare the inherent trade-off between model complexity and the models predictive power, following Occam’s insight that models should only be as complex as necessary. However, theoretical considerations are also important to select the final number of lags to be included in the model. Once the decision of the maximum lagged observations is made we procede in the same fashion previously described in the case of $p=1$ to conclude if $Y$ Granger causes $X$ .

Limitations

The study of Granger causality was initially designed for linear equations. Nowadays, there are extensions to nonlinear cases but those extensions can be more difficult to understand and use, moreover, its statistical meaning is less comprehended. Among the extensions we can find approaches that divide the global nonlinear data into smaller locally linear neighborhoods (Freiwald et al., 1999) or the use of a radial basis function method to perform global nonlinear regression (Ancona et al., 2004)

Another limitation is that one of the assumptions of Granger causality requires that the time series are stationary which means that their mean and variance should maintain constant over time. Non-stationary time series can be transformed in stationary using the method of differentiation. Aditionally, assuming that short windows of non-stationary data produce locally stationary signals is possible to perform the analysis in such windows (Hesse et al., 2003).

A Granger Causality Application

As a student in the field of Communication one of my interests is the study of the information dynamics that people creates on social media. In this section, I want to share an application of the use of Granger causality that I have been working on.

For this example the objective is to analyze if there is a relationship between online communicated emotions in the aftermath of a natural disaster. The approach seeks to understand if the emotions expressed after a tragic event follow a pattern in which it is possible to predict the appearence of some emotions based in the previous expression of other emotions. For example, after an earthquake people express fear initially but once the time passes the expression of emotion changes to sadness so we would like to know if the initial information about fear helps to predict the later appearance of sadness. In this case we collected information from Twitter in the aftermath of the earthquake ocurred in Southern California on July 5, 2019. To assess the emotion each tweet was processed using the Natural Language Understanding tool provided by IBM Watson. This tool analyze the text to assign a value from 0 to for the presence of five emotions: sadness, anger, fear, disgust, and joy.

The procedure has the following steps:

Check stationarity: We upload the data and check the stationarity of the time series.
Stationarity correction: If required we transform the time series to make them stationary.
Lag selection: Based on statistical and theoretical criteria we select the maximum lag for the analysis.
VAR analysis: We conduct an initial multivariate analysis to identify predictive relationships between the five emotions studied.
Granger causality: Once we identify predictive relationship between pairs of emotions we conduct the analysis to determine if those relationships are Granger causal.

You can access to the dataset used in the example here.

View this gist on GitHub

References

Ancona, N., Marinazzo, D., & Stramaglia, S. (2004). Radial basis function approach to nonlinear Granger causality of time series. Physical Review E, 70(5), 056221. https://doi.org/10.1103/PhysRevE.70.056221

Brady, H. E. (2011). Causation and Explanation in Social Science. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199604456.013.0049

Freiwald, W. A., Valdes, P., Bosch, J., Biscay, R., Jimenez, J. C., Rodriguez, L. M., Rodriguez, V., Kreiter, A. K., & Singer, W. (1999). Testing non-linearity and directedness of interactions between neural groups in the macaque inferotemporal cortex. Journal of Neuroscience Methods, 94(1), 105–119. https://doi.org/10.1016/S0165-0270(99)00129-6

Granger, C. W. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society, 424–438.

Hesse, W., Möller, E., Arnold, M., & Schack, B. (2003). The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies. Journal of Neuroscience Methods, 124(1), 27–44. https://doi.org/10.1016/S0165-0270(02)00366-7

Wiener, N. (1956). The theory of prediction. Modern mathematics for engineers. New York, 165–190.

Granger Causality

Pablo M. Flores

ε-Machines

Modes of Information Flow

Transfer Entropy

Instrumental Variables

Structural Causal Modeling

Prediction and Explanation in Social Sciences: Introducing a Set of Useful Methods.

3 thoughts on “Granger Causality”